Answer:
B) 25
Explanation:
Given exponential function:
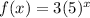
The growth factor between
 and
and
 is 25.
is 25.
To find the growth factor between
 and
and
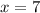
Solution:
The growth factor of an exponential function in the interval
 and
and
 is given by :
is given by :
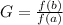
We can check this by plugging in the given points.
The growth factor between
 and
and
 would be calculated as:
would be calculated as:
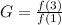
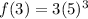
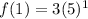
Plugging in values.
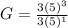
 (On canceling the common terms)
(On canceling the common terms)
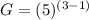 (Using quotient property of exponents
(Using quotient property of exponents
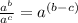 )
)
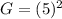
∴
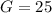
Similarly the growth factor between
 and
and
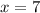 would be:
would be:
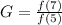
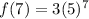
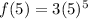
Plugging in values.
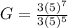
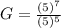 (On canceling the common terms)
(On canceling the common terms)
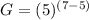 (Using quotient property of exponents
(Using quotient property of exponents
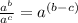 )
)
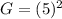
∴
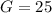
Thus, the growth factor remains the same which is =25.