Question

During a marathon race, a runner’s blood flow increases to 10.0 times her resting rate. Her blood’s viscosity has dropped to 95.0% of its normal value, and the blood pressure difference across the circulatory system has increased by 50.0%. By what factor has the average radii of her blood vessels increased?

Answer 1

To solve the problem it is necessary to apply the equations related to the Poiseuilles laminar flow law, with which the stationary laminar flow ΦV of an incompressible and uniformly viscous liquid (also called Newtonian fluid) can be determined through a cylindrical tube of constant circular section. Mathematically this can be expressed:

`Q = (\Delta P \pi r^4)/(8\eta l)`

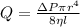
Where:

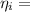`\eta_i =` are the viscosities of the concrete before and after the increase

l = Length of the vessel

`r_1, R_2` = Radio of the vessel before and after the increase

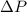`\Delta P`= Change in the pressure

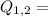`Q_(1,2) =` The rates of flow before and after he increase

Our values are given as:

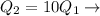`Q_2 = 10Q_1 \rightarrow` 10 times her resting rate

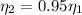`\eta_2 = 0.95\eta_1` 95% of its normal value

`\Delta P_2 = 1.5\Delta P_1` Increase of 50%

Plugging known information to get

`Q_1 = (\Delta P \pi r^4)/(8\eta l)`

`Q_1 8\eta_1 l = \Delta P_1 \pi r_1^4`

`r_1^4 = (Q_1 8\eta_1 l)/(\Delta P_1 \pi)`

`r_1 = ((Q_1 8\eta_1 l)/(\Delta P_1 \pi))^(1/4)`

`r_2 = ((Q_2 8\eta_2 l)/(\Delta P_2 \pi))^(1/4)`

`r_2 = ((10Q_18 * 0.95\eta_1 l)/(1.5\Delta P_1 \pi))^(1/4)`

`r_2 = 1.586r_1`

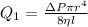
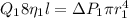
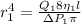
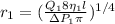
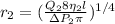
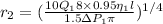
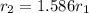
Therefore the factor of average radio of her blood vessels increased is 1.589 the initial factor after the increase.