Answer:
Explanation:
These exponential forms can be written into radicals very easily as long as you remember the rule: The denominator of the rational exponent serves as the index of the radical and the numerator serves as the exponent on the radicand. Let's look at a rational exponent. 3/4 4 would be the index on the radical (the number that sits in the little dip of the radical sign) and 3 is the power on the base. So
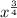 can be written in radical form as
can be written in radical form as
![\sqrt[4]{x^3}](https://img.qammunity.org/2020/formulas/mathematics/high-school/axotv29dyoptesjqm4g8x19b2ua75enlte.png)
Let's do 3^3/2 in your problem. 2 is the index (which is a "normal" square root and you don't need to write a 2 there cuz it's understood that it's a 2 if nothing is there), and 3 is the power on the base, which in our case is a 3. Bases can be numbers OR letters.
![3^{(3)/(2)}=\sqrt[2]{3^3}=√(3^3)](https://img.qammunity.org/2020/formulas/mathematics/high-school/47ud15jwogxj3bln8kcuylabzhzh4mp02n.png)
That does in fact have an actual number answer, but I don't think you are simplifying them yet, only learning to write them from one form to another, so there you go!