Question

Find the minimum or maximum value of f(x) = x2 + 6x +11 .

Answer 1

Therefore the Minimum value of f(x) is 2.

Explanation:

Given:

`f(x)=x^(2) + 6x+11`

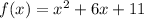
To Find:

minimum or maximum value of f(x)

Solution:

To find minimum or maximum value of f(x)

Step 1 . Find f'(x) and f"(x)

`f(x)=x^(2) + 6x+11`

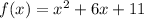
Applying Derivative on both the side we get

`f'(x)=(d(x^(2)))/(dx)+(d(6x))/(dx)+(d(11))/(dx)`

`f'(x)=2x+6+0`

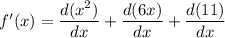
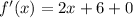
Again Applying Derivative on both the side we get

`f''(x)=(d(2x))/(dx)+(d(6))/(dx)`

`f''(x)=2`

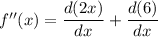
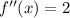
Step 2. For Maximum or Minimum f'(x) = 0 to find 'x'

`2x+6=0\\\\2x=-6\\\\x=(-6)/(2)=-3`

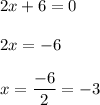
Step 3. IF f"(x) > 0 then f(x) is f(x) is Minimum at x

IFf"(x) < 0 then f(x) is f(x) is Maximum at x

Step 4. We have

`f''(x)=2`

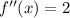
Which is grater than zero

then f(x) is Minimum at x= -3

Therefore the Minimum value of f(x) is 2.