Question

If 2 is added to both the numerator and denominator of a fraction its value becomes half. If two is subtracted from both the numerator and denominator of the same fraction its value becomes 1/3. What is the original fraction"

Answer 1

The original fraction is
`(6)/(14)`.

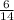Explanation:

Solution,

Let the fraction be'
`(x)/(y)`'.

Where 'x' is the numerator and 'y' is the denominator.

Now according to question, if 2 is added to both the numerator and denominator the value of the fraction becomes 1/2.

So, framing the above sentence in equation form, we get;

`(x+2)/(y+2)=(1)/(2)`

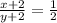
On using cross multiplication method, we get;

`2(x+2)=y+2\\\\2x+4=y+2\\\\2x+4-2=y\\\\\therefore\ y=2x+2\ \ \ \ equation\ 1`

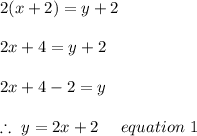
Now according to question, if 2 is Subtracted to both the numerator and denominator the value of the fraction becomes 1/3.

So, framing the above sentence in equation form, we get;

`(x-2)/(y-2)=(1)/(3)`

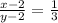
On using cross multiplication method, we get;

`3(x-2)=y-2\\\\3x-6=y-2\\\\3x-y=-2+6\\\\3x-y=4 \ \ \ \ equation\ 2`

Now Substituting the equation 1 in equation 1 we get;

`3x-y=4\\\\3x-(2x+2)=4\\\\3x-2x-2=4\\\\3x-2x=4+2\\\\x=6`

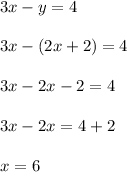
Now Substituting the value of x in equation 1 we get;

`y=2x+2\\\\y=2*6+2 = 14`

Hence The original fraction is
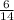`(6)/(14)`.