Answer:
The Amount of money in the account after t years $50
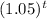
Explanation:
Given as :
The principal deposited into account = $50
The rate of interest = 5% compounded annually
The time period for deposit = t years
Let the amount into account after t years = $A
now, According to question
From compound Interest method
Amount = principal ×
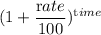
Or, A = $50 ×
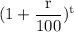
Or, A = $50 ×

Or, A = $50 ×
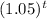
or, A = $50
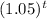
So, The amount in account after t years = A = $50
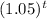
Hence, The Amount of money in the account after t years $50
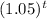 . Answer
. Answer