Question

A researcher believes that 12% of a simple random sample of adults will be able to identify a Toyota Scion by brand and model name. The researcher wishes to estimate with 95% confidence and an allowance for error no greater than 2.5%. How large should the sample be?

Answer 1

Answer: 650

Explanation:

When prior estimate of population proportion is known , then the formula to find the required sample size is given by :-

`n=p(1-p)((z^*)/(E))^2`

, where p= population proportion

E= margin of error

z* = Critical value.

Let p be the proportion of adults able to identify a Toyota Scion by brand and model name.

As per given , we have

p = 12%= 0.12

E= 2.5%=0.025

Critical value for 95% confidence interval : z* = 1.960 [By z-table ]

Then, the required sample size =
`n=(0.12)(1-(0.12))((1.96)/(0.025))^2`

`n=(0.1056)(78.4)^2`

`n=(0.1056)(6146.56)`

`n=649.076736\approx650`

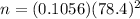
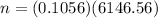
Thus , the required sample size = 650