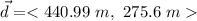Question

A hiker climbs a mountain. Starting at the base of the mountain, he first moved up 520m at a 32.0 degree angle. What is the final displacement of the hiker?

Answer 1

`\displaystyle \vec{d}=<440.99\ m ,\ 275.6\ m>`

Step-by-step explanation:

Displacement Vector

Suppose an object is located at a position

`\displaystyle P_1(x_1,y_1)`

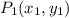
and then moves at another position at

`\displaystyle P_2(x_2,y_2)`

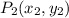
The displacement vector is directed from the first to the second position and can be found as

`\displaystyle \vec{d}=<x_2-x_1\ ,\ y_2-y_1>`

If the position is given as magnitude-angle data ( z , α), we can compute its rectangular components as

`\displaystyle x=z\ cos\alpha`

`\displaystyle y=z\ sin\alpha`

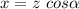
The question describes the situation where the initial point is the base of the mountain, where both components are zero

`\displaystyle P_1(0,0)`

The final point is given as a 520 m distance and a 32-degree angle, so

`\displaystyle x_2=520\ cos32^o= 440.99\ m`

`\displaystyle y_2=520\ sin32^o=275.6\ m`

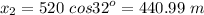
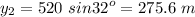
The displacement is

`\displaystyle \vec{d}=<440.99\ m ,\ 275.6\ m>`