Question

Cans of regular Coke are labeled as containing 12 oz12 oz. Statistics students weighed the contents of 88 randomly chosen cans, and found the mean weight to be 12.0912.09 ounces. Assume that cans of Coke are filled so that the actual amounts are normally distributed with a mean of 12.00 oz12.00 oz and a standard deviation of 0.1 oz0.1 oz. Find the probability that a sample of 88 cans will have a mean amount of at least 12.09 oz12.09 oz.

Answer 1

Answer: 0.0055

Explanation:

Let
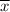`\overline{x}` denotes the sample mean amount that can has.

We assume that cans of Coke are filled so that the actual amounts are normally distributed with a mean of 12.00 oz and a standard deviation of 0.1 oz.

i.e.
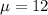`\mu=12` and
`\sigma=0.1`

sample size : n= 8

Then, the probability that a sample of 88 cans will have a mean amount of at least 12.09:

`P(\overline{x}\geq12.09)=1-P(\overline{x}<12.09)\\\\=1-P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(12.09-12)/((0.1)/(√(8))))\\\\=1-P(z<2.5456)\ \ [\because z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}]\\\\=1-0.9945\ \ [\text{By z-table}]\\\\=0.0055`

Hence, the required sample size = 0.0055