Question

A researcher has two percentages and wants to know if the percentages are statistically different. The researcher calculates the z value and finds that it is 4.21. This means that the two percentages: A) Are the same. B) Are not statistically different. C) Have a 421 percent chance of not being different. D) Are statistically different.

Answer 1

`p_v =2*P(Z>4.21) =2.55x10^(-5)`

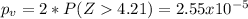
And we can use the following excel code to find it:"=2*(1-NORM.DIST(4.21,0,1,TRUE)) "

With the p value obtained and using the significance level assumed for example
`\alpha=0.05` we have
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the percentage 1 is significantly different from the percentage 2.

D) Are statistically different.

Explanation:

The system of hypothesis on this case are:

Null hypothesis:
`\mu_1 = \mu_2`

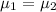
Alternative hypothesis:
`\mu_1 \\eq \mu_2`

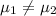
Or equivalently:

Null hypothesis:
`\mu_1 - \mu_2 = 0`

Alternative hypothesis:
`\mu_1 -\mu_2\\eq 0`

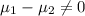
Where
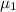`\mu_1` and
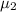`\mu_2` represent the percentages that we want to test on this case.

The statistic calculated is on this case was Z=4.21. Since we are conducting a two tailed test the p value can be founded on this way.

`p_v =2*P(Z>4.21) =2.55x10^(-5)`

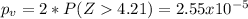
And we can use the following excel code to find it:"=2*(1-NORM.DIST(4.21,0,1,TRUE)) "

With the p value obtained and using the significance level assumed for example
`\alpha=0.05` we have
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the percentage 1 is significantly different from the percentage 2.

And the best option on this case would be:

D) Are statistically different.