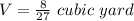Answer:
Option D is correct.
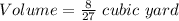
Explanation:
Let V be the volume of hay in each stack
Given:
Length of the each stack is
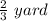
And Jay stores hay in cubic stacks on his farm.
The volume of the cone is.
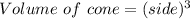
Now, we substitute value of length of stack in above equation.
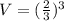
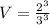
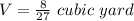
Therefore, the volume of hay in each stack is