Answer:
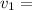 -15.03m/s
-15.03m/s
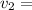 25.01 m/s
25.01 m/s
Step-by-step explanation:
Using the conservation of the linear momentum:
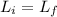
So, for axis x:
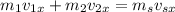
where
 is the mass of the block A,
is the mass of the block A,
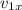 is the velocity in x of the block A,
is the velocity in x of the block A,
 is the mass of the block B,
is the mass of the block B,
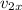 is the velocity in x of the block B,
is the velocity in x of the block B,
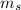 the mass of the block A and B together and
the mass of the block A and B together and
 the velocity in x of both blocks after the collition.
the velocity in x of both blocks after the collition.
Replacing values:
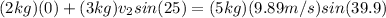
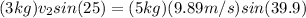
Solving for
 :
:
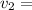 25.01 m/s
25.01 m/s
At the same way, for axis y:

where
 is the mass of the block A,
is the mass of the block A,
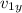 is the velocity in y of the block A,
is the velocity in y of the block A,
 is the mass of the block B,
is the mass of the block B,
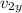 is the velocity in y of the block B,
is the velocity in y of the block B,
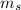 the mass of the block A and B together and
the mass of the block A and B together and
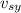 the velocity in y of both blocks after the collition.
the velocity in y of both blocks after the collition.
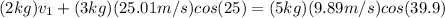
solving for
 :
:
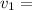 -15.03m/s
-15.03m/s
it is negative because we set the north as positive.