Question

A boat traveled 153 miles downstream and back. The trip downstream took 9 hours. The trip back took 17 hours. What is the speed of the boat in the still water. What is the speed of the current?

Answer 1

Speed of boat in still water is 13 miles per hour and speed of current is 4 miles per hour

Solution:

Let s = the speed of the boat in still water in miles/hour

Let c = the speed of the current in miles/hour

Formula to remember:

If the speed of a boat in still water is s miles/hr and the speed of the current is c miles/hr, then:

Speed downstream = (s + c) miles per hour

Speed upstream = (s - c) miles per hour

Given:

boat traveled 153 miles downstream and back

distance for downstream = 153 miles

distance for upstream = 153 miles

time taken for downstream = 9 hours

Time taken for upstream = 17 hours

The relation between speed, distance and time is given as:

`distance = speed * time`

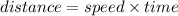
For downstream:

`153 = (s + c) * 9`

`s + c = (153)/(9) = 17`

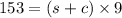
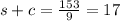
s + c = 17 ------- eqn 1

For upstream:

`153 = (s - c) * 17\\\\s - c = (153)/(17) = 9`

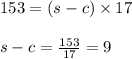
s - c = 9 ------- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "s" and "c"

Add eqn 1 and eqn 2

s + c = 17

s - c = 9

(+) -------------

2s = 26

s = 13

Substitute s = 13 in eqn 1

13 + c = 17

c = 17 - 13 = 4

c = 4

Thus the speed of boat in still water is 13 miles per hour and speed of current is 4 miles per hour