Answer:
Step-by-step explanation:
mass of bullet, m = 130 g
Force, F = 11000 + 13000 x - 28000 x²
(a) the work done by the gas is given by



W1 = 1904522.08 J
(b) the work done by the gas is given by

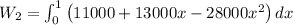
[tex]W_{1}=11000\times 1+6500\times 1-9333.33\times 1
W2 = 8166.67 J
W1 / W2 = 233.2