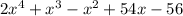 expression represents the area of Dylan’s room
expression represents the area of Dylan’s room
Solution:
Given that,
Length of room =

Width of room =
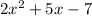
To find: Expression that the area (lw) of Dylan’s room
Since bedroom is generally of rectangular shape, we can use area of rectangle
The area of rectangle is given as:
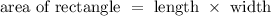
Substituting the given expressions of length and width,

We multiply each term inside first parenthesis with each term inside the second parenthesis.
So it becomes,
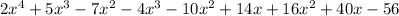
Now combine like terms,
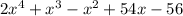
Thus the above expression represents the area of Dylan’s room