Question

100 Quick and EASY POINTS to make if you can help me!

Rules are:
You HAVE to answer it with proof
Dont put things like "I need more steps" just to get points
Or i WILL report you and you will lose the points
And If ya get it wrong when i turn it in, I will delete your answer because i dont want other ppl with wrong answers
IF YOU SEE A PERSON ALREADY ANSWERED, DONT ANSWER IT.
these are the simple rules if you dont wanna get banned :>
Peace

Answer 1

x=125

Explanation:

x>0, x=125

`log_(2) 8 = log_(5) x\\log_(2)2^(3) = log_(5) x\\3=log_(5) x\\log_(5) x=3\\x=5^(3) \\x=125`

Answer 2

`x=125`

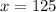
Explanation:

We have the equation:

`\displaystyle \log_2{24}-\log_2{3}=\log_5x`

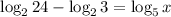
And we want to find the real value of x.

First, we can use the Quotient Property of Logarithms, which states:

`\displaystyle \log_ba-\log_bc=\log_b{(a)/(c)`

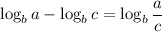
Therefore, we can rewrite our left-hand side as:

`\displaystyle \Rightarrow \log_2{(24)/(3)}=\log_5x`

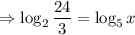
Divide:

`\log_28=\log_5x`

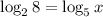
Evaluate the left-hand side (2³=8).

`3=\log_5x`

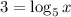
By the definition of a logarithm, this means that:

`5^3=x`

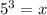
Evaluate:

`x=125`

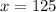
Our final answer is 125.