Question

There are 6 students. 2 of them are chosen for the position of president and Vice President. How many ways do we have to choose the students from the 6 students?

Answer 1

We have 15 ways to chose 2 students for the position of president and Vice President

Solution:

Given that,

There are 6 students. 2 of them are chosen for the position of president and Vice President.

To find: number of ways we have to choose the students from the 6 students

So now we have 6 students, out of which we have to choose 2 students

As we just have to select the students. We can use combinations here.

In combinations, to pick "r" items from "n" items, there will be
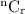`^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}` ways

`^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}=(n !)/((n-r) ! r !)`

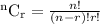
Then, here we have to pick 2 out of 6:

Total students = n = 6

students to be selected = r = 2

`\begin{aligned} 6 C_(2) &=(6 !)/((6-2) ! 2 !) \\\\ 6 C_(2) &=(6 !)/(4 ! 2 !) \\\\ 6 C_(2) &=(6 * 5 * 4 * 3 * 2 * 1)/(4 * 3 * 2 * 1 * 2 * 1) \\\\ 6 C_(2) &=15 \end{aligned}`

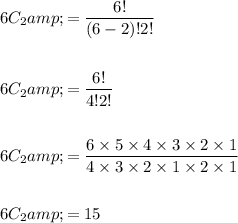
Thus we have 15 ways to chose 2 students for the position of president and Vice President