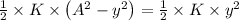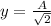Answer:
Step-by-step explanation:
Let the amplitude is A.
Displacement, x = one third of the amplitude = A/3
The total energy of the body executing Simple Harmonic Motion is given by
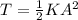
(a) Kinetic energy of the particle executing SHM is given by
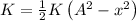
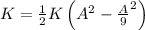
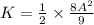
So, the ratio of kinetic energy to the total energy is given by
K / T = 8 / 9
(b) Potential energy of a particle executing SHM is given by
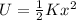
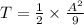
So, the ratio of potential energy to the total energy is given by
U / T = 1 / 9
(c) Let at a displacement y the kinetic energy is equal to the potential energy