Question

In considering medical insurance for a certain operation, let X be the amount (in $) paid for the doctor and let Y be the amount (in $) paid to the hospital. In the past, the variances have been Var(X) = 8,100,Var(Y) = 10,000, and Var(X+Y) = 20,000. Due to increased expenses, it was decided to increase the doctor’s fee by $500 and increase the hospital charge Y by 8%. Calculate the variance of the new total claim, i.e. the variance of X + 500 + 1.08Y

Answer 1

`Var[X+500+1.08Y]=Var[X+1.08Y]= 1^2 (8100) + 1.08^2 (10000) +2(950)=21664`

Explanation:

Previous notation

Let X and Y random variables we have the following properties given:

Var(X) = 8100

Var(Y)= 10000

Var(X+Y)=20000

And we are interested on find the variance for the following random variable X+500+1.08Y

`Var(X+500+1.08Y)`

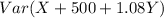
We have the following properties when we have a sum of random variables

If Y is a random variable:

`Var [\sum_(i=1)^n c_i Y_i]=\sum_(i=1)^n c^2_i Var(Y_i) +2 \sum_(i=1)^n \sum_(j=i+1)^n c_i c_j Cov [Y_i, Y_j]` (1)

This property is derived from the expected value of the random variable Y:

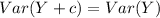`Var(Y+c) =Var(Y)` (2)

Solution to the problem

Using the (2) property we have:

`Var[X+500+1.08Y]=Var[X+1.08Y]`

And using the property (1) we have:

`Var[X+1.08Y]= 1^2 Var[X] + 1.08^2 Var[Y] +2Cov(X,Y)`

But we don't know the covariance for the two random variables so we can use the Var(X+Y) to find Cov(X,Y) like this:

`Var[X+Y]= Var[X]+Var[Y] +2Cov(X,Y)`

Solving for Cov(X,Y) we got:

`2Cov(X,Y)=Var[X+Y] -Var[X] -Var[Y]`

`Cov(X,Y)=(20000-10000-8100)/(2)=950`

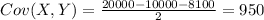
And then we can use this in order to find Var[X+500+1.08Y] like this:

`Var[X+500+1.08Y]=Var[X+1.08Y]= 1^2 (8100) + 1.08^2 (10000) +2(950)=21664`