Question

AB = 6x DC = x + 15 AD = 9 BC = 3y Quadrilateral ABCD is a parallelogram if both pairs of opposite sides are congruent. Show that quadrilateral ABCD is a parallelogram by finding the lengths of the opposite side pairs. A) 9, 6 B) 12, 9 C) 18, 9 D) 18, 12

Answer 1

Therefore the lengths of the opposite side pairs.

C) 18, 9

Explanation:

Given:

Quadrilateral ABCD is a parallelogram

AB = 6x

DC = x + 15

AD = 9

BC = 3y

TO Find:

AB = ?

BC = ?

Solution:

Quadrilateral ABCD is a parallelogram ..........Given

∴ Both pairs of opposite sides of a Parallelogram are congruent.

∴ AB = DC and AD = BC

substituting the values we get

`6x=x+15\\6x-x=15\\5x=15\\x=(15)/(5)\\ x=3\\and\\9=3y\\y=(9)/(3)\\ y=3`

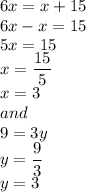
substituting the x' and 'y' values we get

`AB= 6* 3=18\\and\\BC=3* 3=9`

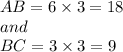
Therefore the lengths of the opposite side pairs.

C) 18, 9