Question

In order to determine the average price of hotel rooms in Atlanta. Using a 0.1 level of significance, we would like to test whether or not the average room price is significantly different from $110. The population standard deviation is known to be $16. A sample of 64 hotels was selected. The test statistic (z) is calculated and it is 1.74. We conclude that the average price of hotel rooms in Atlanta is NOT significantly different from $110. (Enter 1 if the conclusion is correct. Enter 0 if the conclusion is wrong.)

Answer 1

Answer: 0

Explanation:

Let
`\mu` be the average room price.

By considering the given problem , we have

`H_0:\mu=110`

`H_0:\mu\\eq110`

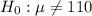
Since alternative hypothesis two-tailed , so the test is a two-tailed test.

Also, the population standard deviation is known to be $16, so we perform z-test.

The test statistic (z) is calculated and it is 1.74.

P-value = 2P(Z>|z|) = 2P(Z>1.74)

=2(1-P(Z≤1.74)) [∵ P(Z>z)=1-P(Z≤z)]

=2(1- 0.9591) [By z-table]

=0.0818

Decision : Since P-value (0.0818) < Significance level (0.1), so we reject null hypothesis.

We conclude that the average price of hotel rooms in Atlanta is significantly different from $110 at 0.1 level of significance.

It means the given conclusion is wrong.

Hence, the correct option is 0.