Question

Which of the following is a step in simplifying the expression x multiplied by y to the power of 4 over x to the power of negative 5 multiplied by y to the power of 5, the whole to the power of negative 3.? (5 points)

Group of answer choices

x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.

x to the power of negative 3 multiplied by y, the whole over x to the power of negative 8 multiplied by y to the power of 2.

x to the power of negative 3 multiplied by y, the whole over x to the power of negative 5 multiplied by y to the power of 5.

x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of negative 5 multiplied by y to the power of 5.

Flag this Question
Question 6

Answer 1

x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.

Explanation:

Given:

`((xy^4)/(x^(-5)y^5) )^(-3)`

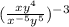
We need to simplify the equation.

As while solving these kind of problems, keep in mind the following Law on Indices:

1.
`(a^m)^n=a^(mn)`

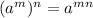
Applying the same we get;

`(x^(-3)(y^4)^(-3))/((x^(-5))^(-3)(y^5)^(-3))\\\\(x^(-3)y^(4*-3))/(x^(-5*-3)y^(5*-3)) \\\\(x^(-3)y^(-12))/(x^(15)y^(-15))`

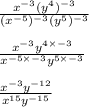
Final Answer:

x to the power of negative 3 multiplied by y to the power of negative 12, the whole over x to the power of 15 multiplied by y to the power of negative 15.