Question

Four items are on sale at a local store. A shirt was originally $9.50 and now is $7.60. A pair of jeans were $25.00, and now they are priced $20.00. A pair of boots were $55.00, and they are on sale for $44.00. Do these regular and sale prices represent a proportional relationship

Answer 1

Answer:YES

Explanation:

Answer 2

Answer : Yes, regular and sale prices represent a proportional relationship.

Step-by-step explanation :

We have to determine the ratio of regular and sale prices of shirt, jeans and boots .

A shirt was originally $9.50 and now is $7.60.

`\frac{\text{Regular price}}{\text{Sale price}}=(\$ 9.50)/(\$ 7.60)`

`\frac{\text{Regular price}}{\text{Sale price}}=(5)/(4)`

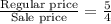
A pair of jeans were $25.00, and now they are priced $20.00.

`\frac{\text{Regular price}}{\text{Sale price}}=(\$ 25.00)/(\$ 20.00)`

`\frac{\text{Regular price}}{\text{Sale price}}=(5)/(4)`

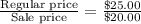
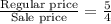
A pair of boots were $55.00, and they are on sale for $44.00.

`\frac{\text{Regular price}}{\text{Sale price}}=(\$ 55.00)/(\$ 44.00)`

`\frac{\text{Regular price}}{\text{Sale price}}=(5)/(4)`

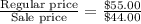
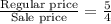
From this we conclude that, all the items are in same ratio that means the regular and sale prices represent a proportional relationship.

Hence, yes, regular and sale prices represent a proportional relationship.