Question

In ΔABC, ∠C measures 46° and the values of a and c are 10 and 9, respectively. Find the remaining measurements of the triangle, and round your answers to the nearest tenth. ∠A = 82.2°, ∠B = 62.8°, b = 17.1 ∠A = 53.1°, ∠B = 80.9°, b = 12.4 ∠A = 53.1°, ∠B = 80.9°, b = 17.1 ∠A = 82.2°, ∠B = 62.8°, b = 12.4

Answer 1

∠A = 53.1°, ∠B = 80.9°, b = 12.4

Explanation:

i got it right on my test

Answer 2

`\angle{A}=53.1^(\circ)`

`\angle{A}=80.9^(\circ)`

`b=12.4`

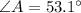
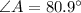
Explanation:

Please find that attachment.

We have been given that in ΔABC, ∠C measures 46° and the values of a and c are 10 and 9, respectively.

First of all, we will find measure of angle A using Law Of Sines:

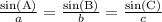`\frac{\text{sin(A)}}{a}=\frac{\text{sin(B)}}{b}=\frac{\text{sin(C)}}{c}`, where, A, B and C are angles corresponding to sides a, b and c respectively.

`\frac{\text{sin(A)}}{10}=\frac{\text{sin(46)}}{9}`

`\frac{\text{sin(A)}}{10}=(0.719339800339)/(9)`

`\frac{\text{sin(A)}}{10}=0.0799266444821111`

`\frac{\text{sin(A)}}{10}*10=0.0799266444821111*10`

`\text{sin(A)}=0.799266444821111`

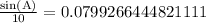
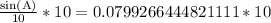
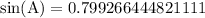
Upon taking inverse sine:

`A=\text{sin}^(-1)(0.799266444821111)`

`A=53.060109978759^(\circ)`

`A\approx 53.1^(\circ)`

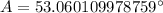
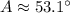
Therefore, the measure of angle A is 53.1 degrees.

Now, we will use angle sum property to find measure of angle B as:

`m\angle{A}+m\angle{B}+m\angle{C}=180^(\circ)`

`53.1^(\circ)+m\angle{B}+46^(\circ)=180^(\circ)`

`m\angle{B}+99.1^(\circ)=180^(\circ)`

`m\angle{B}+99.1^(\circ)-99.1^(\circ)=180^(\circ)-99.1^(\circ)`

`m\angle{B}=80.9^(\circ)`

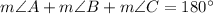
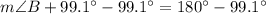
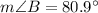
Therefore, the measure of angle B is 80.9 degrees.

Now, we will use Law Of Cosines to find the length of side b.

`b^2=a^2+c^2-2ac\cdot\text{cos}(B)`

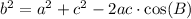
Upon substituting our given values, we will get:

`b^2=10^2+9^2-2(10)(9)\cdot\text{cos}(80.9^(\circ))`

`b^2=100+81-180\cdot 0.158158067254`

`b^2=181-28.46845210572`

`b^2=152.53154789428`

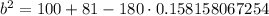
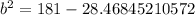
Upon take square root of both sides, we get:

`b=√(152.53154789428)`

`b=12.3503663060769173`

`b\approx 12.4`

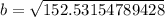
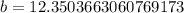
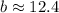
Therefore, the length of side b is approximately 2.4 units.