Question

Iodine-131, t1/2 = 8.0 days, is used in the diagnosis and treatment of thyroid gland diseases. If a laboratory sample of iodine-131 initially emits 9.95 × 1018 β particles per day, how long will it take for the activity to drop to 6.22 × 1017 β particles per day?

Answer 1

32,0 days.

Step-by-step explanation:

The radioactive decay follows:

`N_(t) = N_(0)e^{(-0.693t)/(t_(1/2))`

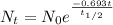
Where Nt is the concentration in a time t (6,22x10¹⁷), N₀ is the initial concentration (9,95x10¹⁸) Half life time is 8,0 days and t is the time it take to drop this concentration. Replacing:

`6.22x10^(17) = 9,95x10^(18)e^{(-0.693t)/(8 days)`

`0,0625 = e^{(-0.693t)/(8days)`

`ln 0,0625 = {(-0.693t)/(8days)`

`-2,77*8days = -0.693t`

`-22,2days = -0.693t`

`32,0days = t`

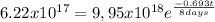
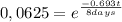
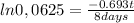
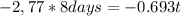
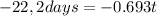
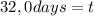
It take 32,0 days

I hope it helps!