Question

Find the vertical asymptote(s) of f of x equals quantity 5 x squared plus 3x plus 6 end quantity over quantity x squared minus 100.

x = −5, 10
x = −10, 10
x = 5, −10
x = −5, 5

Answer 1

x = 10 and x = -10

Explanation:

Given the function

`f(x)=(5x^2+3x+6)/(x^2-100)`

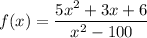
This function is undefied when the denominator equals to 0. Find these values for x:

`x^2-100=0\\ \\(x-10)(x+10)=0\\ \\x-10=0\ \ \text{or}\ \ x+10=0\\ \\x=10\ \ \text{or}\ \ x=-10`

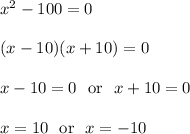
This means that vertical lines x = 10 and x = -10 are vertical asymptotes (the graph of the function f(x) cannot meet these lines because this function is undefined at x = 10 and x = -10)