Question

3x^2+2x+5=0
Quadratic equation

Answer 1

The quadratic equation has a form of

`ax^2+bx+c=0\wedge a\\eq0`

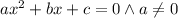
We have

`3x^2+2x+5=0`

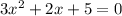
Hence our coefficients are

`a=3,b=2,c=5`

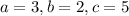
Now to find a solution we have to look at the equation, since equation has no apparent solution given by the factorisation we are forced to use quadratic formula.

`x_(1,2)=-(b^2\pm√(b^2-4ac))/(2a)`

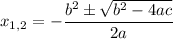
Put in the data and simplify a bit

`</p><p>x_(1,2)=-(2^2\pm√(2^2-4\cdot3\cdot5))/(2\cdot3) \\</p><p>x_(1,2)=-(4\pm√(-56))/(6)\in\mathbb{C}</p><p>`

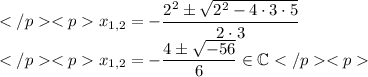
And we get two complex solutions

`</p><p>x_1=\boxed{-(4)/(6)-(56)/(6)i} \\</p><p>x_2=\boxed{-(4)/(6)+(56)/(6)i}</p><p>`

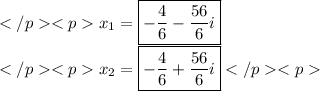
Hope this helps.

r3t40

Answer 2

Explanation:

use formula

(-b+√b2-4ac)/2a

a=3, b=2 , c=5

(-2+√4-4×3×5)/2×3

(-2+√-56)/6

(-2+2√-14)/6

(-2 +2√14i)/6