Question

DetermiOne of the lines in the Balmer series of the hydrogen atom emission spectrum is at 397 nm. It results from a transition from an upper energy level to n=2. What is the principal quantum number of the upper level?ne the initial energy level, ninitial from which the electron in the hydrogen relaxed from to the final energy level, nfinal , 4, if the emitted light has a frequency equal to 74 x 1012 (1/sec). Is this wavelength in the visible region of the electromagnetic spectrum?

Answer 1

a)n =7 , b) n = 5

Step-by-step explanation:

The energy levels of the hydrogen atom is described by the Bohr model

`E_(n)` = - 13.606 1/n²

This equation energy is given in elector volts and n is an integer

A transition occurs when the electro sees from a superior to a lower state

E₀ -
`E_(n)` = -13.606 (1/
`n_(f)`² - 1/n₀²)

Let's apply this expression

n₀ = 2

Let's look for the energy of the different levels and subtract it

n₀
`E_(n)` (eV)

1 -13,606

2 -3.4015

3 - 1.5118

4 -0.850375

5 -0.54424

6 -0.3779

7 -0.2777

The wavelength of the transition is 397 nm = 397 10⁻⁹ m

The speed of light is related to wavelength and frequency

c = λ f

The Planck equation gives the energy of a transition

E = h f

E = h c /λ

Let's calculate

E = 6.63 10⁻³⁴ 3 10⁸/397 10⁻⁹

E = 5.01 10⁻¹⁹ J

Let's reduce to eV

E = 5.01 10⁻¹⁹ J (1 eV / 1.6 10⁻¹⁹ J)

E = 3.1313 eV

Let's examine the possible transitions from the initial level ni = 2

ΔE =
`E_(2)` -
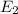`E_(n)` = -3.1313

En = 3.13 -3.4015

`E_(n)` = 0.2702 eV

When examining the table we see that the level that this energy has is the level of n = 7

Part B the transition is in the infrared

The frequency is 74 10¹² Hz

We use the Planck equation

E = h f

E = 6.63 10⁻³⁴ 74 10¹²

E = 4.9062 10⁻²⁰ J

E = 4.9062 10⁻²⁰ / 1.6 10⁻¹⁹

E = 0.3066 eV

We look for the level with the energy difference

ΔE = E₄-
`E_(n)` = 0.3066

`E_(n)` = 0.3066 - 0.85037

`E_(n)` = -0.54376 eV

When examining the table this energy has the level n = 5, therefore from this level the transition occurs