Answer:
The future principal amount invested is $13,660.27 .
Explanation:
Given as :
The Amount that saved for future = A = $20,000
The bank applied rate of interest = r = 10%
The time period of loan = t years
Now As Miranda's daughter is 14 year now, and she will give money when her daughter turns 18
∴ The time period of loan = t = 4 years
Let the future principal amount invested = $p
Now, From Compound Interest method
Amount = principal ×
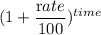
Or, A = p ×
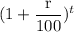
Or, $20,000 = p ×
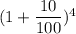
Or, $20,000 = p ×
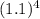
Or, $20,000 = p × 1.4641
∴ p =
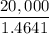
i.e p = $13,660.269
So, The future principal amount invested = p = $13,660.27
Hence, The future principal amount invested is $13,660.27 . Answer