Question is Incomplete, Complete question is given below;
Fiona wrote the linear equation y = 2/5 X -5. When Henry wrote his equation they discovered that his equation had all the same Solutions as fionas. which equation could have been Henry's.
A. X- 5/4y =25/4
B. X-5/2y=25/4
C. X-5/4y =25/4
D. X- 5/2y=25/2
Answer:
D.
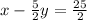
Explanation:
Given:
Fiona's equation =
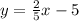
We have to figure out which of the choices equals the equation given,
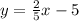
Now we could solve each of the answer choices for
 , but since each choice is in the format
, but since each choice is in the format
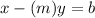 , we can put the given equation in that format too.
, we can put the given equation in that format too.
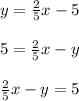
Now in given choices x doesn't have any terms with it.
Hence we will make x term as 1 by dividing 5/2 on both side we get;
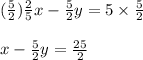
Hence Henry equation will be
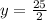 .
.