Question

What type of triangle is created by the three cities?

The distance between city A and city B is 22 miles. The
distance between city B and city C is 54 miles. The distance
between city A and city C is 51 miles.
an acute triangle, because 222 + 542 >512
an acute triangle, because 222 + 512 >542
an obtuse triangle, because 222 + 542 >512
an obtuse triangle, because 222 + 512 >542

Answer 1

The answer is B on Edge 2020 Thank me Later!

Explanation:

I did the Exam

Answer 2

An acute triangle, because
`22^2 + 51^2 >54^2`

Explanation:

Given:

The distance between city A and city B is 22 miles.

The distance between city B and city C is 54 miles.

The distance between city A and city C is 51 miles.

thus we have a triangle ABC with side lengths :

AB = 22 miles (shortest side)

BC= 54 miles (longest side)

AC = 51 miles (shorter side)

For an obtuse triangle :

`(Shorter\ side)^2+(Shortest\ side)^2<(Longest\ side)^2`

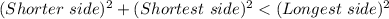
For acute triangle :

`(Shorter\ side)^2+(Shortest\ side)^2>(Longest\ side)^2`

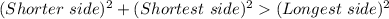
Comparing sum of squares of shorter sides with the square of longest side:

`AB^2+AC^2=22^2+51^2=484+2601=3085`

`BC^2=54^2=2916`

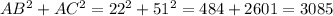
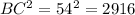
We see that:

`22^2+51^2>54^2`

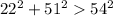
Thus, the condition
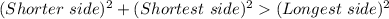`(Shorter\ side)^2+(Shortest\ side)^2>(Longest\ side)^2` fulfills proving this triangle to be an acute triangle.