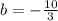Question

6

3b3 + 10b2 = 0
A) Find the GCF
B) Factor out the GCF
C) What are the solutions?

Answer 1

Explanation:

The GCF is the common "thing" in each one of the terms in our polynomial. Since 3 doesn't divide evenly out of 10, 3 is not a GCF. But b-squared is common in both. So for part A. the GCF is b-squared.

part B. Factor out the GCF:

`b^2(3b+10)=0`

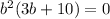
For part C. What are the solutions? The solutions are found in the Zero Product Property which states that if the factors of a polynomial, when multiplied together, equal 0, then either one of the factors or both of the factors have to equal 0 because 0 times anything equals 0. That means that

`b^2=0` and/or 3b + 10 = 0

Solving the first equation:

`b^2=0` and b = 0.

Solving the second equation:

3b + 10 = 0 and

3b = -10 so

`b=-(10)/(3)`