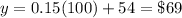Answer:
100 miles
Explanation:
Let
x ----> the number of miles driven
y ---> the total cost
we know that
The linear equation in slope intercept form is equal to
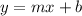
where
m is the slope or unit rate of the linear equation
b is the y-intercept or initial value
In this problem we have
First Plan
The slope is equal to
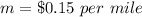
The y-intercept is
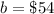
so
The linear equation is
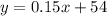 -----> equation A
-----> equation A
Second Plan
The slope is equal to
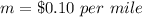
The y-intercept is
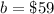
so
The linear equation is
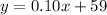 -----> equation B
-----> equation B
To find out for what amount of driving do the two plans cost the same, equate equation A and equation B
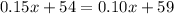
solve for x
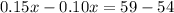
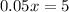
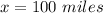
Find the cost
for x=100 miles
substitute in equation A or equation B (the cost is the same)