Answer:
Measure of Angle 5 = 150 degree.
Explanation:
Given line g and h are parallel lines.
Let angle measuring
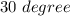 be a.
be a.
From figure we can see that
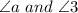 both are Linear Pair Postulate,
both are Linear Pair Postulate,
i.e.
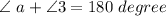
So,


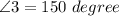 ------------(equation 1)
------------(equation 1)
Now,
 are alternate interior angles, and alternate interior angles are equal.
are alternate interior angles, and alternate interior angles are equal.
i.e.
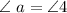
Therefore
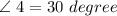 ------------(equation 2)
------------(equation 2)
Now,
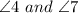 both are Linear Pair Postulate,
both are Linear Pair Postulate,
i.e.
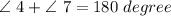
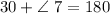 ------------------(from equation 2)
------------------(from equation 2)
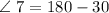
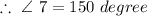 ---------(equation 3)
---------(equation 3)
Now,
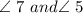 are vertically opposite angles, and vertically opposite angles are equal.
are vertically opposite angles, and vertically opposite angles are equal.
So,
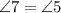
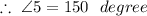 -----------------(from equation 3)
-----------------(from equation 3)