Answer:
The angle of depression of the power line making with ground and connected to the top of building is 40.11° .
Explanation:
Given as :
The length of the wire connected to the top of building = h = 340 meters
The distance of the power line away from base of building = x = 260 meters
Let The angle of depression = Ф
Now, from figure
cos angle =
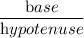
I.e cosФ =
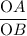
Or, cosФ =

Or, cosФ =
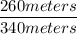
Or, cosФ =
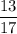
∴ Ф =
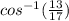
or, Ф =
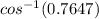
So , Ф = 40.11°
So, The angle of depression from the ground = Ф = 40.11°
Hence, The angle of depression of the power line making with ground and connected to the top of building is 40.11° . Answer