Question

As part of a screening process, computer chips must be operated in an oven at 145 °C. Ten minutes after starting, the temperature is 65 °C. After 15 minutes, the temperature is 85 °C.

What is the temperature after 23 minutes?

Answer 1

Explanation:

This is an initial condition problem using natural logs to solve. The formula for this is

`y=Ce^(kt)`

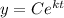
where y is the temp after t time, e is Euler's number, C is the initial value, and k is the constant of proportionality. We have 2 unknowns we need to solve for before we can answer the actual question about the temp after 23 minutes. We also can come up with 2 equations to solve for these unknowns:

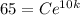`65=Ce^(10k)` and
`85=Ce^(15k)`

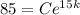
Since our initial value, C, is the same for both equations, we can solve for C in one of the equations and sub it into the other in order to solve for k:

If

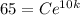`65=Ce^(10k)`, then

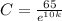`C=(65)/(e^(10k))`, which, equivalently, is

`C=65e^(-10k)`

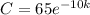
Subbing that value into the other equation:

`85=65e^(-10k)(e^(15k))`

Divide both sides by 65 to get

`(85)/(65)=e^(-10k+15k)` (that uses the fact that we are multiplying like bases together so we add their exponents), and

`(85)/(65)=e^(5k)`

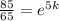
Now take the natural log of both sides to get

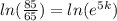`ln((85)/(65))=ln(e^(5k))` which simplifies to

`.2682639866=5k` so

k = .0536527973

Now we have our k value. We can sub it into one of our equations to solve for C now:

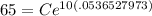`65=Ce^(10(.0536527973))` and

`65=Ce^(.536527973)`

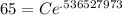
Raise e to that power to get

65 = C(1.710059171) so

C = 38.01038064

Now we have enough info to solve for the temp after 23 minutes:

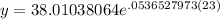`y=38.01038064e^(.0536527973(23))` and

`y=38.01038064e^(1.234014338)`

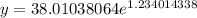
Raise e to that power to get

y = 38.01038064(3.434991111) so

y = 130.565 degrees after 23 minutes