Question

The function C(x) = 25.50x + 50 models the total cost for a cleaning company to clean a house, where x is the number of hours it takes to clean the house. What is the average rate of change of the function between 3 hours and 9 hours? A. $17.00 per hour B. $25.50 per hour C. $31.05 per hour D. $42.15 per hour

Answer 1

The average rate of change is $25.5 per hour, option B.

Explanation:

Average Rate of Change

When we are explicitly given some function C(x), we sometimes need to know the rate of change of C when x goes from
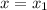`x=x_1` to
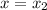`x=x_2`. It can be computed as the slope of a line .

`\displaystyle m=(C(x_2)-C(x_1))/(x_2-x_1)`

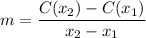
The provided function is

`C(x)=25.50x + 50`

We are required to compute the average rate of change between the points

`x_1=3\ ,\ x_2=9`

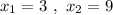
Let's compute

`C(3)=25.50(3) + 50=126.5`

`C(9)=25.50(9) + 50=279.5`

`\displaystyle m=(279.5-126.5)/(9-3)`

`\displaystyle m=(153)/(6)=25.5`

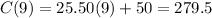
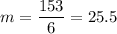
The average rate of change is $25.5 per hour, option B.