Answer:
48 kg
Step-by-step explanation:
Given that the two wires are of same material, so their value of young's modulus will be same
Assuming that the wires are cylindrical in shape
As radius of the first wire is half that of the second wire and therefore the area of cross-section of the first wire will be one-fourth of the second wire( ∵ wire is cylindrical, the cross-sectional part will be circle and the area of the circle = π × r² )
As the volume is same for both wires
∴ π × (
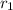 )² ×
)² ×
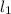 = π × (
= π × (
 )² ×
)² ×
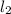
Here
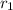 is the radius of the first wire
is the radius of the first wire
 is the radius of the second wire
is the radius of the second wire
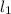 is the length of the first wire
is the length of the first wire
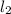 is the length of the second wire
is the length of the second wire
⇒ π × ((
 )² ÷ 4) ×
)² ÷ 4) ×
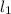 = π × (
= π × (
 )² ×
)² ×
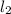 (∵ radius of first wire is half that of the second wire)
(∵ radius of first wire is half that of the second wire)
By cancelling the same terms on both sides
we get
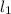 = 4 ×
= 4 ×
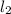
⇒ Length of first wire will be four times of the length of second wire
Strain is defined as the elongation per unit length
Strain in first wire = ΔL ÷
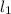 = ΔL ÷ (4 ×
= ΔL ÷ (4 ×
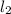 )
)
where ΔL is the elongation of the wire which in this case is same in both wires
Strain in second wire = ΔL ÷
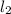
∴ Strain in second wire is four times of strain in first wire
Stress = F ÷ A
where F is the force perpendicular to the cross-sectional area
A is the area of cross-section
Force in first wire =
 × g
× g
where
 is the mass hanged to the first wire
is the mass hanged to the first wire
g is the acceleration due to gravity
Force in second wire =
 × g
× g
where
 is the mass hanged to the second wire
is the mass hanged to the second wire
g is the acceleration due to gravity
Let
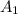 be the cross-sectional area of first wire
be the cross-sectional area of first wire
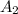 be the cross-sectional area of second wire
be the cross-sectional area of second wire
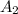 = 4 ×
= 4 ×
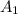 (∵ cross=sectional area of the wire = π × (radius of the wire)² )
(∵ cross=sectional area of the wire = π × (radius of the wire)² )
Stress in first wire = (
 × g) ÷ (
× g) ÷ (
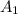 )
)
Stress in second wire = (
 × g) ÷ (
× g) ÷ (
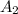 ) = (
) = (
 × g) ÷ (4 ×
× g) ÷ (4 ×
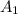 )
)
Young's modulus is defined as Stress per unit strain
As Young's modulus is same for both wires, Stress per unit strain must be same for both wires
Stress per unit strain of first wire = ((
 × g) ÷ (
× g) ÷ (
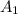 )) ÷ (ΔL ÷ (4 ×
)) ÷ (ΔL ÷ (4 ×
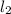 ))
))
Stress per unit strain of second wire = ((
 × g) ÷ (4 ×
× g) ÷ (4 ×
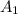 )) ÷ (ΔL ÷
)) ÷ (ΔL ÷
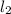 )
)
By equating them we get
 = 16 ×
= 16 ×

⇒
 = 16 × 3 = 48 kg
= 16 × 3 = 48 kg
∴
 = 48 kg
= 48 kg