Question

Given the function g(x) = x^3 − (8+1)x^2-4(9+2)x+(5x2-1) determine where the function is quickly(slowly) increasing (decreasing)

Answer 1

hence g(x) is increasing at point x= 3+14i,3-14i

Explanation:

given, g(x)=x^3-(8+1)x^2-4(9+2)x+5x2-1

g(x)=x^3-9x^2-44x+10x-1

g(x)=x^3-9x^2-34x-1

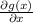`(\partial g(x))/(\partial x)`=3x^2-18x-34

for increasing and decreasing function,

3x^2-18x-34=0

x=3+14i
`\geq`0

x=3-14i
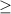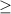`\geq`0

hence g(x) is increasing at point x= 3+14i,3-14i answer