Question

Based on the information on the diagram, what is the measure of angle ADC?​

Answer 1

73°

Explanation:

Given: BD=BE

∠DBE= 50°

∠EAC= 42°

DE//AC and AE=CD

Attach is the new drawn diagram with M point.

∵ we know BD=BE, ∴ ∠BDE=∠BED= x ( taking x as unknown angle)

Remember, sum of triangle= 180°

Now, ∠BDE+∠BDE+∠DBE= 180°

⇒
`x+x+50= 180`

⇒
`2x+50= 180`

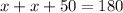
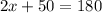
Subtracting both side by 50, then dividing both side by 2

∴
`x= (130)/(2)= 65`°

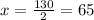We know, ∠MAC= ∠MCA= 42° (∵AM=MC)

Next, ∠EDC=DCA= 42° ( ∵ Alternate interior angle as we know DE//AC )

Now, we have ∠EDC= 42°, ∠BDE= 65°

∴
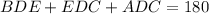`BDE+EDC+ADC= 180`° (∵sum of straight line= 180°)

⇒
`65+42+ADC= 180`°

⇒
`107+ADC= 180`°

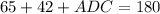Subtracting both side by 107

∴∠ADC=
`180-107= 73`°

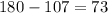∴∠ADC= 73°