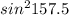Answer:
1 ) sin 165°
2 ) cos 330°
3 ) Tan 157.5°
4 )
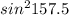
Explanation:
1 )
Given expression is
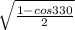
We know that
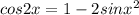
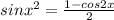
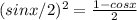
So the first expression is sin (330/2)° =sin 165°
2 )
GIven expression is
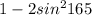
We know that
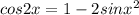
So the result is cos 330°
3 )
Given expression is
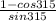
We know that
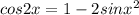
Also we know that sin2x = 2sinxcosx
So The numerator becomes
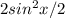 . and the denominator becomes as
. and the denominator becomes as
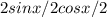
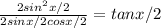
So the result is Tan 157.5°
4 )
Given expression is
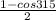
We know that
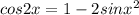
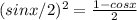
So the result is