Question

Sarawong's school is selling tickets to the annual talent show. On the first day of ticket sales the

school sold 14 adult tickets and 14 child tickets for a total of $224. The school took in $44 on the
second day by selling 2 adult tickets and 6 child tickets. Find the price of an adult ticket and the
price of a child ticket.

Answer 1

Price of the adult ticket is $13

Price of the child ticket is $3

Explanation:

Lets x be the adult ticket and y be the child ticket.

Given:

School sold 14 adult tickets and 14 child tickets for a total of $224, so the first equation is.

`14x+14y=224`-------------(1)

And the school took in $44 on the second day by selling 2 adult tickets and 6 child tickets, so the second equation is.

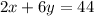`2x+6y=44`---------------(2)

We find the price of an adult ticket and the price of a child ticket by solving above system of equation.

Now, equation 2 multiplied by 7.

`7(2x+6y=44)`

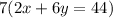
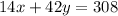`14x+42y=308`---------(3)

Now, equation 1 subtracted by equation 3.

`14x+42y=308`

`14x+14y=224`

-______________

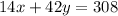
14x is cancelled in both equations, so we get the equation.

`28y=84`

`y=(84)/(28)`

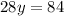
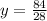
y = 3

Now, we substitute y = 3 in equation 2.

`2x+6(3)=44`

`2x+18=44`

`2x=44-18`

`2x=26`

`x=(26)/(2)`

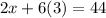
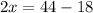
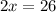
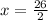
x = 13

Therefore, the price of the adult ticket is $13 and the price of the child ticket is $3.