Question

LUIMT Problems

1. Liliana has $2.10 in nickels and quarters in her purse. She has 12 more nickels than
quarters. How many coins of each type does she have?​

Answer 1

Liliana has 13 quarters and 25 nickels in her purse.

Step-by-step explanation:

Let's assume that Liliana has x quarters and x+12 nickels.

Quarters are worth 25 cents each, so the total value of quarters is 25x cents.

Nickels are worth 5 cents each, so the total value of nickels is 5(x+12) cents.

According to the problem, the total value of quarters and nickels is $2.10, which is equal to 210 cents.

Therefore, we have the equation: 25x + 5(x+12) = 210.

By simplifying and solving the equation, we find that x = 13.

So, Liliana has 13 quarters and 13+12 = 25 nickels.

Answer 2

The coins of each type are, 17 nickel coins and the 5 quarter coins.

Step-by-step explanation:

Given:

Liliana has $2.10 in nickels and quarters in her purse.

She has 12 more nickels than quarters.

Now, to find the coins of each type she have.

Let the number of nickels be
`x.`

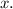
Let the number of quarters be
`x-12.`

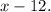
The total worth of coins = $2.10.

The value of a quarter is $0.25 and the value of a nickel is $0.05.

According to question:

`0.25(x-12)+0.05(x)=2.10`

⇒
`0.25x-3+0.05x=2.10.`

⇒
`0.30x-3=2.10`

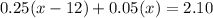
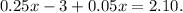
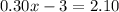
Adding both sides by 3 we get:

⇒
`0.30x=5.10`

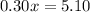
Dividing both sides by 0.30 we get:

⇒
`x=17.`

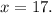
The number of nickels = 17.

Now, to get the number of quarters we put value of
`x` :

`x-12`

`=17-12=5.`

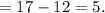
The number of quarters = 5.

Therefore, the coins of each type are, 17 nickel coins and the 5 quarter coins.