Answer:
The slope of line r is

Explanation:
Given as :
The points that line p contains is A ( - 1 , 4 ) and B ( 3 , - 5 )
Let The slope of line p =

So,
 =
=
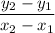
Or ,
 =
=

Or,
 =
=
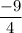
Now, Again ,
Line q is parallel to the line p
let The slope of line q =

So, for parallel lines
slope of lines are equal
I.e
 =
=

∴
 =
=
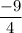
Again ,
Line r is perpendicular to the line q
let The slope of line r =
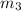
So, for perpendicular lines
The product of the slopes of two line = - 1
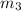 ×
×
 = - 1
= - 1
or,
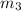 ×
×
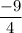 = - 1
= - 1
or,
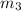 =
=
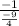
∴
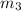 =
=

So, The slope of line r =
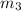 =
=

Hence , The slope of line r is
 . Answer
. Answer