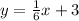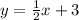The set of equations that represent this situation is:
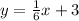
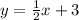
Solution:
Let "x" represent the smaller number
Let "y" represent the larger number
Given that,
Six times a larger number is equal to the sum of a smaller number and 18
Here "times" represents multiplication
Six times a larger number = sum of a smaller number and 18
6 x larger number = smaller number + 18
6y = x + 18
Thus,
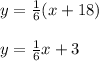
Also given that difference of twice the larger number and the smaller number is 6
twice the larger number - smaller number = 6
2y - x = 6
Thus,
2y = x + 6
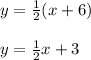
Thus the set of equations that represent this situation is: