Answer:
-7
Explanation:
Lets assume the number Peggy is thinking of be "x".
Now as given, when twice the number is added to three times one more than the number. We can write it as
∴
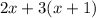 --- Equation 1
--- Equation 1
Again, it is given that Peggy gets the same result as when she multiplies four times one less than the number.
∴
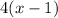 -- equation 2
-- equation 2
Next, we can equate both the equation 1 and 2 as it is given that result is same.

Let´s distribute 3 into
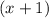 and 4 into
and 4 into

⇒
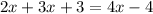
⇒
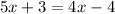
Subtract both side by 4x and 3
∴
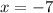
∴ Peggy was thinking of -7