Question

Let θ (in radians) be an acute angle in a right triangle and let x and y, respectively, be the lengths of the sides adjacent to and opposite θ. Suppose also that x and y vary with time. At a certain instant x=9 units and is increasing at 9 unit/s, while y=5 and is decreasing at 19 units/s. How fast is θ changing at that instant?

Answer 1

Step-by-step explanation:

According to question

tan θ = y / x

Differentiate with respect to t on both the sides

`Sec^(2)\theta * (d\theta )/(dt)=(x* dy/dt-y* dx/dt)/(x^(2))`

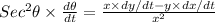
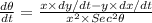`(d\theta )/(dt)=(x* dy/dt-y* dx/dt)/(x^(2)* Sec^(2)\theta)` .... (1)

According to question,

tan θ = 5 / 9

So, Sec θ = 10.3 / 9 = 1.14

dx/dt = 9 units/s

dy/dt = 19 units/s

Substitute the values in equation (1), we get

`(d\theta )/(dt)=(9* 19-5* 9)/(81* 1.14^(2))`

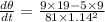
dθ/dt = 1.2 units/s