Question

For a given piece of code, the hit ratio of first cache is 0.1 and the hit ratio of second cache is 0.3. The time required to access the first cache is 10 nanoseconds, the second cache is 100 nanoseconds, and the time to access the underlying physical memory is 1 microsecond, what is the effective memory access time for the piece of code?

Answer 1

effective memory access = 658 ns

Explanation:

GIven data:

Effective memory access time is given as

`= [H_1*T_1]+[(1-H_1)*H_2*T_2]+[(1-H_1)(1-H_2)*H_m*T_m]`

from the data given above we have

`H_1 = 0.1`

`H_2 = 0.3`

`T_1 = 10 ns`

`T_2 = 100 ns`

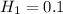
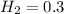
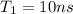
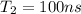
hit rate,
`H_m = 1 ns`

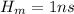
access time
`= T_m = 1000 ns`

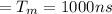
Plugging all information in above formula to get the effective memory access

`= 0.1* 10 + 0.9* 100+ 0.9 * 0.7* 1 * 1000`

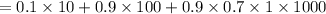
= 1+27+ 630

=658 ns