Answer:
The amount invested at 9% was $3,200 and the amount invested at 13.5% was $1,800
Explanation:
Let
x ----> the amount invested at 9% (first fund)
5,000-x ----> the amount invested at 13.5% (second fund)
Remember that
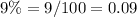
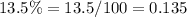
The total interest earned is equal to
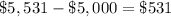
we know that
The amount earned by the first fund at 9% plus the amount earned by the second fund at 13.5% must be equal to $531
so
the linear equation that represent this situation is equal to
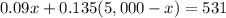
solve for x
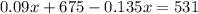
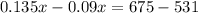
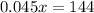
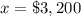
so
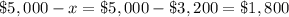
therefore
The amount invested at 9% was $3,200 and the amount invested at 13.5% was $1,800