Question

An object is thrown directly downward from the top of a very tall building. The speed of the object just as it is released is 17.1 m/s. After being thrown, the object falls freely due to gravity. Neglect air resistance and calculate the distance, in meters which the object covers between times t1 = 3.32 s and t2 = 5.08 s after it is thrown.

Answer 1

distance cover is = 102.53 m

Step-by-step explanation:

Given data:

speed of object is 17.1 m/s

`t_1 = 3.32 sec`

`t_2 = 5.08 sec`

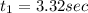
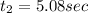
from equation of motion we know that

`d_1 = vt_1 + (1)/(2) gt_1^2`

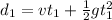
where d_1 is distance covered in time t1

so
`d_1 = 17.1 * 3.32 + (1)/(2) 9.8 * 3.32^2`=

`d_1 = 110.78 m`

`d_2 = vt_2 + (1)/(2) gt_2^2`

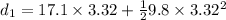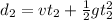
where d_2 is distance covered in time t2

`d_2 = 17.1 * 5.08 + (1)/(2)*9.8 * 5.08^2`

`d_2 = 213.31 m`

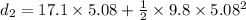
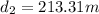
distance cover is = 213.31 - 110.78 = 102.53 m